|
Real-Time Visualization of the Quantum
Mechanical Atomic Orbitals
The orbital images on this page represent the shape of the
atomic orbitals. The clouds you see are the probability
distribution of an electron bound to a Hydrogen nucleus.
These images were created using Atom
in a Box, a
scientific and educational program that aids in visualizing
the Hydrogenic atomic orbitals, a prime and otherwise unwieldy
example of quantum mechanics.
|
|
|
NOTE: First announced at the 1998 Conference on
Computational Physics held in Granada, Spain, I am a
student winner in Computers In
Physics' Ninth Annual Software Contest with Atom
in a Box. Full descriptions of the prize winners
are in CIP's
Nov/Dec 1998 issue. This now makes me the only person to
have been a student winner twice in a row in
CIP's Software Contest.
In addition, Apple has been kind
enough to write an article
about Atom in a Box in their inaugural
issue of Apple University Arts. Do you speak Dutch?
Prata svenska?
Sprechen Sie Deutsch?
Habla español?
Parlez-vous Français?
Parlate italiano?
Also, this program appears in a
12-minute streaming RealVideo clip at the UCLA Department
of Design.
In addition to the many kind individuals who have
registered, I thank all those who registered from
institutions such as: Massachusetts Institute of
Technology, Pacific Lutheran University, U. C. Davis,
Georgia Institute of Technology, Pennsylvania State
University, University of Houston, Wesleyan University,
University of Missouri - St. Louis, Purdue University,
Millikin University, West Virginia University,
Karl-Franzens-Universität Graz, Universität Bern,
Washington State University, Southwest Missouri State
University, Douglas High School, San Joaquin Delta
College, Maine Maritime Academy, Kalamazoo College,
Southwestern University - Georgetown, Texas, Haverford
College, Florida A&M University, Nagoya University,
Miami University, Virginia Tech, Yale University, Bob
Jones University, Cornell University, Kyoto University,
Utah State, Institute for Advanced Study at Princeton,
Snow College, Hammond High School, Reed College,
University of Washington, Wooster College, Colorado
School of Mines, the Wellington School, the University
of Southern Mississippi, Harvey Mudd College. Many
people have registered from outside the United States:
Japan, United Kingdom, Canada, Austria, Switzerland,
Belgium, Germany, and Italy.
Through word of mouth, I have heard of my program in
use at Caltech, U. C. Santa Cruz, Stanford, Harvard, and
others. |
Unlike other tools in this category, this program raytraces
through a three-dimensional cloud density that represents the
wavefunction's probability density and presents its results in
real-time (up to 48 frames per second on Mac G3s; even faster on the latest hardware).
The user interface is very interactive and provides a wide
degree of flexibility.
It contains all 140 eigenstates up to the n=7 energy level
and the allowed spectral transitions between those
eigenstates. The Mac version also allows a state formed by a superposition
(see below)
of up to eight of those eigenstates allowing for over 3
trillion possible states and can display a
wavefunction as a picture of a cloud, use color as phase, plot
in red-cyan left/right for 3D glasses, and slice the
wavefunction.
You can see more example
images at the bottom of the page.
What is Quantum Mechanics?
One of the great advances in human knowledge of the
twentieth century is the birth of the theory of Quantum
mechanics. It has led to some of the most common technologies
used today, including the little transistors that make up the
computers you're using to read this. One of the mysteries it
revealed was the structure of the atom. Classical mechanics
could not properly explain the existence of the atom. Because
there was nothing to stop electrons from spiralling in to the
nucleus, it predicted that all atoms would immediately destroy
themselves in a spectacular high-energy blast of radiation.
Well, that obviously doesn't happen. Quantum mechanics
describes that the electron (and all of the universe for that
matter) exists in any of a multitude of states. The particular
physical situation determines what and how many states there
are. Borrowing from some of the techniques in mathematics,
physicists organize these states into a particular set of
mathematically convenient states called "eigenstates".
Eigenstates are good to use because what makes one eigenstate
different from another usually has a physical meaning. They
also can make an horribly difficult problem managable. These
and other phenomena in Quantum mechanics predict that
possiblities in physical phenomena have distinct separations
(e.g., "quantum leaps") and that energy transport exists as
indivisible packets, called "quanta". Hence the name: Quantum
Mechanics.
What are Orbitals?
By applying these techniques to the hydrogen atom,
physicists are able to precisely predict all of its
properties. The electron eigenstates around the nucleus are
called "orbitals", in a rough correspondence with how the Moon
orbits the Earth. We find that these states do not allow the
electron to crash into the nucleus, but instead find
themselves in any combination of these orbital eigenstates.
These orbitals' physical structure describe effects from how
atoms bond to form compounds, magnetism, the size of atoms,
the structure of crystals, to the structure of matter that we
see around us.
Visualizing these states has been a challenge, because the
mathematics that describe the eigenfunctions are not simple
and the states are a three-dimensional structures. The
standard convention has the orbital eigenstates indexed by
three interrelated integer indicies, called n, l, and m. Their
range and interdependence comes out of the math in deriving
the eigenstates. n can range from 1 to infinity. l can range
from 0 to n-1. m can range from -l to +l. They also have
physical meaning. The energy of the state, which is negative
because the electron is bound to the nucleus, depends only on
n and increases as n increases. l refers to the amount of
angular momentum the electron has due to its "orbit" around
the nucleus. l is not equal to the amount of angular momentum
but goes up as angular momentum goes up. m determines how much
of the angular momentum is in the z direction. (However, the
rest of the angular momentum is not l minus m or
anything that simple. That's a long story that I can't fit
here. Look in a Quantum textbook (a good one is A Modern
Approach to Quantum Mechanics by John S. Townsend), take a
course, or talk to a physics professor.)
 |
What's here for me?
I have written a Macintosh application that displays atomic
orbitals in real-time. Rather than just a plot of the
spherical harmonics, as is shown in many Quantum mechanics
textbooks, this program displays the electron orbital as a
cloud. The cloud's density is determined by the orbital's
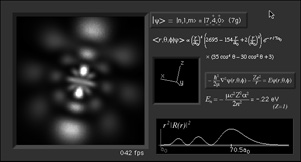
probability density for the electron. There are three examples
on this web page: The one at the top is the n=3, l=2, m=0
state; the screenshot above has n=7, l=4, m=0; the first
example below is n=6, l=4, m=1. (The quality is poor so that
they wouldn't take too long to download over the Internet.
They'll look even worse if you are not using Millions of
colors to view it. The program looks quite a bit better, trust
me.) With the program, you can rotate the orbital around in
real time. If you have red-cyan 3-D glasses, you can see it in
3-D too. The program has all the orbital eigenstates up to
n=7, which is the highest occupied shell for the ground states
of the heaviest elements, e.g., Uranium, Plutonium, etc.
You can download the application
from the links below and have a look. The program is computation
intensive. For individual users, the v1.x Mac application is US
$20 shareware.
Pricing of the later versions are on the App Store.
You can read the details in the about box or the
Read Me. Also supplied are example orbital files.
Platform Availability
| Mac | | iPhone and iPod Touch | | iPad |
| |
| |
|
 Atom in a Box 2.0
- Universal 2 release of Atom in a Box version 2.0
for Apple Silicon and Intel Macs running on macOS "Big Sur" 11.2 or later.
|
Universal 2
|
Rewritten from the ground up, v2 of Atom in a Box uses SwiftUI 2.0
and multicore to reach new capabilities the previous code could never do.
 Atom in a Box 1.1
- (468 kB) Universal Application 2006 release of Atom in a Box version 1.1
for PowerPC and Intel Macs running on OS X 10.3.9 until macOS "Mojave" 10.14.
|
|
After Mojave, Apple ended support for the Carbon API this app uses.
If you're not sure if it'll run on your macOS, you may download it so you can test.
This code base will receive no further updates.
In 2006, the Universal Binary version included the following enhancements:
QuickTime export of the orbital animation, in addition to PICS.
Endian conversions for file and disk access. Adapted source to Xcode.
OS X-compliant application
and file icons and plst data. Correction of an issue with sound buffers
for the orbital sound. New recognition of horizontal and vertical scroll
wheels, so now you can use the Mighty Mouse's scroll ball to rotate the
orbital.
Known issue in the Universal version: On most Macs, OS X 10.4.x places a 60
fps governor on QDFlushPortBuffer, consequently limiting the speed with which
AiB can display its animation. One should be aware of that before making speed
comparisons. Hint: increase the Samples setting to make the calculations more
challenging.
For OS 9 and pre-OS X 10.3.9, we also provide a
Carbon CFM version of AiB 1.1 (324 kB).
Atom
in a Box, a.k.a. Orbitals, v1.0.7 (~472k PowerPC only,
CarbonLib required),
v1.0.6 will run on both OS 9 (with CarbonLib) and OS X. The
latest pre-Carbon version of Atom in a
Box, v1.0.4 is no longer supported. See the READ ME for
more details.
Atom in a
Box, a.k.a. Orbitals, v1.0.4, for Motorola 680x0 is available,
but it's really slow (not real-time: 3 seconds per frame on a
//ci).
|
|
Atom in a Box -
With the debut of the App Store,
the release of Atom in a Box for the iPhone and iPod Touch.
|
The orbital will reorient and interact using
the iPhone's multitouch interface and accelerometer.
Quantum mechanical data is presented graphically and mathematically
via the iPhone's intuitive user interface.
|
|
|
See the App Store for pricing and availability for your country.
|
|
Atom in a Box HD -
Atom in a Box for the iPad
released in the App Store.
Rewritten from scratch for HD resolutions, this App presents the orbital in an immersive environment where it will
reorient and interact using
the iPads's multitouch interface, magnetometer, and accelerometer.
It can calculate, render, and display all 2109 eigenstates up to the n=18 energy level.
See the App Store for pricing and availability for your country.
|
|
| |
See the
Atom in a Box iOS Online FAQ for
Version History.
Reviewers:
Please email your request and your background info (e.g., your web site)
to feedback @ daugerresearch.com
to obtain a review copy.
|
A Short Gallery of Animated Orbitals
|
This is the quantum state where n=6, l=4, and m=1: |
 |
|
This is an equal superposition of the |3,2,1> and
|3,1,-1> eigenstates: |
 |
|
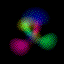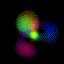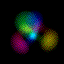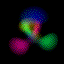This is an equal superposition of the |3,2,2> and
|3,1,-1> eigenstates: |
 |
|
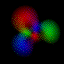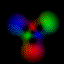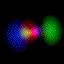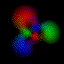This is an equal superposition of the |4,3,3> and
|4,1,0> eigenstates: |
 |
|
