| Dauger Research Vault | ||
| Tutorial | |||||||||||||||||||||
|
|
||||||||||||||||||||
|
Parallelization
There are two distinct issues one encounters when using parallel computers to solve computational problems. The first is how to construct the parallel computer, use it, launch jobs, and maintain the parallel computer. The second issue is how to go about organizing your computational problem so that it can be solved on a parallel computer.
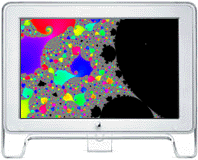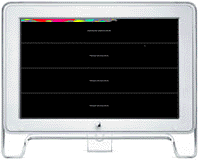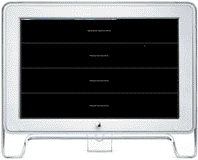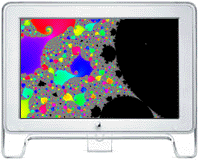
Although volumes have been written on the issues involved in that second issue, this page is meant to provide an introduction to those parallelization issues, that of writing parallel code or parallelizing code. Automatic parallelization of code has been an active research topic in scientific computing for the last two decades, but such codes, except for very special cases, typically achieve little of the potential benefit of parallel computing. So far, the human contribution has been essential to produce the best performing parallel codes. Candidates for Parallelization Any operations that take longer than a minute to complete are good candidates for parallelization. Simpler operations like drawing to the screen or writing email or primitive drawing would probably not be appropriate applications to parallelize. However, large CMYK-RGB image conversions, large scientific simulations, analyses of large datasets, rendering complex 3D graphics, video compositing and editing, or large scale search or structure traversing problems would be appropriate to parallelize because they could see benefits from parallel computing. Partitioning the Problem A key to parallelizing an application is choosing the appropriate partitioning of the problem. The choice must be made so to minimize the amount of time spent communicating relative to the time spent computing. One can think of the partitioning being in a direction, or on an "axis" or degree of freedom of the problem. The size of the partitioning should not be so small that the code experiences high communication overhead, but should be small enough so that the problem can be divided into at least as many pieces as there are processors. Simplest Parallelization - divide and conquer Suppose the application was required to compute a two-dimensional image and the values of its pixels can be computed completely independently and in any order. The simplest way to parallelize such a problem would be to cut the image into strips and assign a node to compute a strip each until the problem is finished. Many applications can be partitioned into pieces like these and implemented on a parallel computer. The older fractal demonstration codes partitioned the problem along the y-axis of the image. Hence, each processor computed a horizontal strip of the image, then they sent the results back to node 0, which then assembled the pieces to complete the solution for the user. Later it was seen that the fractal problem was sometimes cut into pieces of uneven difficultly for identical processors.
This load-balancing algorithm handles irregularities in the problem, the processors, and the network using one algorithm. In addition, the Fresnel Diffraction Explorer assigns the lines in a order so that the user can see the image evolve into progressively finer detail as it is being computed. The user is better able to see an approximation of the diffraction pattern well before it is complete. The goal is to be user-friendly even while running in parallel. The approach of dividing the problem into independent sections is appropriate for a variety of other interesting computational problems. Rendering a single image of a three-dimensional scene would also be appropriate to parallelize this way. But choosing to partition along the vertical axis is not the only way. If such an application instead had to render many 3D scenes in a time sequence, it could be more appropriate to divide the problem along the time axis or timeline.
 Similarly, a video editing application could partition the final high-resolution render along its timeline, and perhaps choose the partitioning at the edit points in the video rather than choosing N pieces for N nodes. Many searching or structure traversing problems could be parallelized by partitioning sections of the data set at points appropriate to the nature of the data set. Searching a very large document for a word could be accomplished by assigning each node its piece of the document and collecting the results of each nodes search of its section. Chess programs and other game codes often search a "game tree", a representation of the consequences of one player's move, then the next move, and so forth, for desirable outcomes to determine the "best" next move. One could parallelize such a code by assigning nodes to begin at branches not far from the base of the tree, but far enough that there will be enough branches to assign enough work to keep all the nodes busy. Node 0 then combines the results of those searches to produce its final answer. The above problems are often collected into a class that is sometimes called "trivially parallelizable". That is, these problems are relatively straightforward to parallelize because the work performed by each node does not depend on each other, or at least has very little dependence. An extreme example of a "trivially parallelizable" problem is SETI@Home, where the computational nodes could be computing pieces of the problem for hours before sending brief replies back to a server. The extreme nature of the SETI@Home problem makes it appropriate for implementation over the Internet on a wide scale. As noble as the goal of SETI@Home is, however, their implementation is practical only for the few types of computational problems whose communications demands are so low. Parallelizing Tightly-Coupled Scientific Code - more difficult, but achievable A computational problem that is impossible to parallelize given enough time and clever ingenuity has yet to be conceived, but nonetheless scientific computational problems can be the most difficult to parallelize. Effective and efficient parallel codes have been created to solve problems in materials engineering, chemistry, biology, quantum mechanics, high-energy physics, galaxy evolution, mathematics, economics, game theory, and many more. Below we provide a taste of the more advanced parallelization algorithms that are needed. Particle-based plasma simulations are an excellent example of a scientific problem that was successfully parallelized but was not trivial to implement. A plasma is a collection of charged particles interacting through mutual electromagnetic fields. These particles are not merely influenced by their nearest neighbors, but are usually influenced by all the other particles. (Another important part of the code is the field solve which can require some form of a parallelized FFT. That's a chapter in itself, so we'll focus only on the particles here.)
The bulk of the computation is accomplished when each node computes the trajectories of each of the particles in its partition. However, at each time step some of the particles will drift far enough to leave its node's partition of space and cross into the neighboring partitions. That node then assembles messages containing all the particles that now belong to its neighbors and sends those messages to the appropriate nodes. Likewise, that node receives messages from its neighbors about particles that are its responsibility.
What also makes this problem nontrivial is its communication demands. On a cluster, nodes running plasma codes often requires a few megabytes per second of continuous bandwidth and communication many times per second to coordinate its work. Distributing this work over the Internet, with potentially long delays and limited bandwidth, is unlikely to be practical, while local 100BaseT networking usually satisfies these demands. A Mac cluster becomes an ideal choice to for these kinds of tightly-coupled parallel codes. Getting to Know MPI To get started writing code, you are welcome to study the source code examples in the Pooch Software Development Kit. If this is your first time writing parallel code, you should probably start by looking over and running the knock.c or knock.f examples. That code demonstrates how to use the most fundamental MPI calls that start up (MPI_Init) and tear down (MPI_Finalize) the MPI environment, access how many tasks are in the cluster (MPI_Comm_size), identify your task (MPI_Comm_rank), send a message (MPI_Send), and receive a message (MPI_Recv). With only those six calls, it is possible to write very complex and interesting parallel codes. After you have understood those routines, you can explore the routines for asynchronous message passing (MPI_Irecv, MPI_Isend, MPI_Test, MPI_Wait). Those calls allow your code to send and receive messages and compute simultaneously. Properly utilization of those calls will make it possible for your code to take optimal advantage of parallel computing. The pingpong.c and pingpong.f examples in the SDK demonstrate how to use those calls. Those 10 calls are the most important parts of MPI and could very well be all that you need. After that, MPI provides other calls that build on the above 10 and can be thought of as convenience routines for common patterns in parallel computing, such as collective calls that perform broadcasts or matrix-style manipulation or collect and rearrange data. We also provide six tutorials on writing and developing parallel code: Parallel Knock, Parallel Adder, Parallel Pascal's Triangle. Parallel Circle Pi, Parallel Life, and Visualizing Message Passing. The first tutorial shows how to perform basic message passing, and the last exhibits parallel code alongside a visualization of the resulting message passing. The remaining four show conversion of single-processor code into parallel code. Together, these documents demonstrate many fundamental issues encountered when writing for parallel computers. Further Reading As we have stated, many volumes exist on how one would go about writing parallel code, so we can only list a handful of those. In Search of Clusters by Gregory F. Pfister is a good book that compares and contrasts various types of parallel computers and explores the issues involved with coding for such machines. Pfister's discussion in Sections 9.3 through 9.5 comparing the application of shared-memory versus message-passing programming to a simple solution of LaPlace's equation is very insightful. Using MPI by William Gropp, Ewing Lusk and Anthony Skjellum is a good reference for the MPI library. The following references provides a detailed description of many of the parallelization techniques used the plasma code:
You're welcome to read more about parallel computing via the Tutorials page.
|
|||||||||||||||||||||