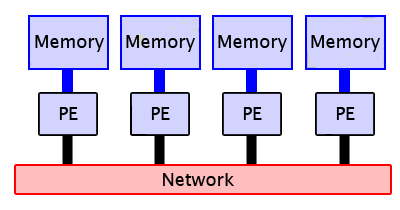
Parallel Programming Paradigms - Processors and Memory

When writing a program for a computer it is important that the writer know what the basic capabilities of the hardware are so that the writer can make fundamental assumptions about its structure. When writing code for parallel computers, the writer must bear in mind a particular paradigm, or way of thinking, regarding the structure of the hardware. That paradigm implies basic assumptions about how fundamental hardware components, such as processors and memory, are connected to one another. These basic assumptions are crucial to writing functionally correct and efficient parallel code.

We describe in this article the programming paradigm used in modern parallel computing and how this paradigm came to be. Its development is best understood both in light of the architecture of the machines that run such codes and in contrast other parallel computing paradigms, so these are also explored. In order for people to write parallel applications and direct machines utilizing parallel computing with many processors, the establishment of a flexible and fully capable way to program machines is essential. We provide examples below to illustrate the issues involved when designing and running such codes.

What is Always True about Parallel Computing

By definition, parallel computing always involves multiple processors (or computing elements or processing elements (PEs) or cores; below we use these terms interchangeably). That's something on which all of its practitioners can agree. Because we must derive parallel computers from today's incarnation of von Neumann-architected Turning machines, the computer has memory, which is also agreed.

But the next question is: Where is the memory? How is it organized? When there is only one processor, it is clear that the processor needs to access all its memory, but when there are multiple, how should these processors be connected to memory? Should the memory likewise be made "parallel" in some sense, or should the memory remain as one and homogeneous, as it was with one processor? This is a fundamental question of parallel computer design because it has ultimately enormous, and potentially expensive, consequences for hardware, software, and their designers and builders.

Parallel Computing of the 1990's - The Great Schism

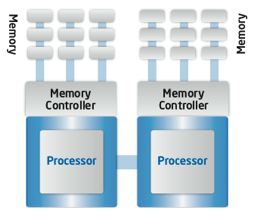
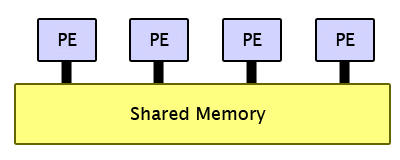
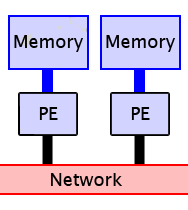
Delineated by that very question, parallel computing paradigms of the 1990's falls into two major categories: Shared Memory - Usually via threads, all processors can access all memory directly at any time Distributed Memory - A processor can access only its own memory, but processors can share data using message passing. Access is the key, and, for processors, access means they are allowed to read and write. In a distributed memory system, a processor, in effect, "owns" its own memory. For such processors to share data they must pass messages, much like how people make a phone call. In contrast, processors on a shared memory system can easily read and write the same location in memory in any order, like people being able to read, erase, and write on the same whiteboard. While a leaving a message for the other processor is easy, resolving potential confusion is left to the program writer. Problems whose parts are completely separated from and indepdent of one another are trivial to parallelize. For such problems running on shared or distributed memory matters little because the problem is already self-partitioned; easy problems are easy to run in parallel. But most interesting problems have some irreducible interaction between them. The two different memory models or parallel computing paradigms encourage two very different ways to handle interactions. 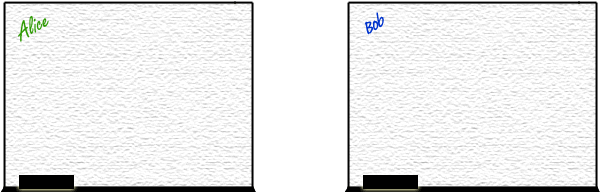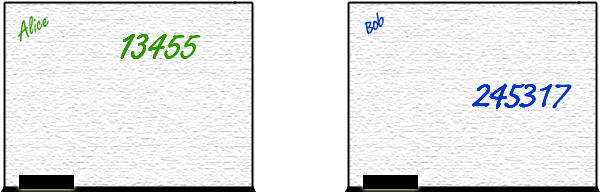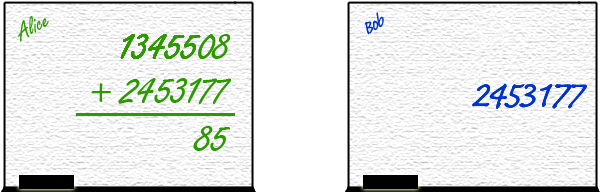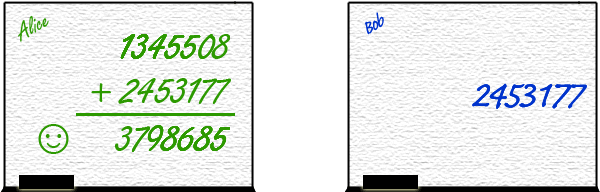To illustrate the basic issue, consider the following analogy: two people, Alice and Bob, working at a whiteboard. The whiteboard corresponds to the shared memory and Alice and Bob are two processors sharing that memory. Suppose Alice needs to add two numbers to produce the final answer. She can compute the first number, but the second number is in fact a result from Bob. Alice and Bob each require time to compute their numbers, so the idea is that Bob, once he has it, will write his number on the second line of Alice's final summation. Then when Alice has written the first number, she will sum her number with Bob's number and the calculation is complete. Seems simple, right?

Maybe not. A great deal of uncertainty is how long Alice and Bob will take to compute their part of the problem. Depending on the nature of the input, or the time of day, or if Bob or Alice get distracted, stop to take a drink, or other random or pseudorandom influences Alice and Bob might complete their numbers at slightly different times.

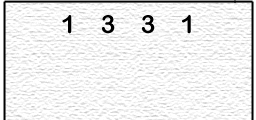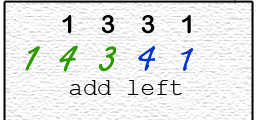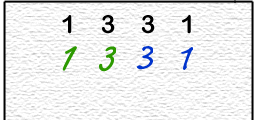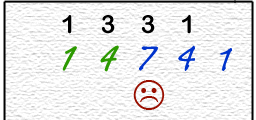
Why is this important? We have three ways this photo finish could end up.

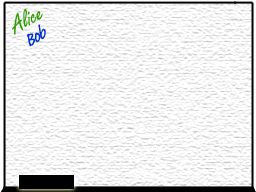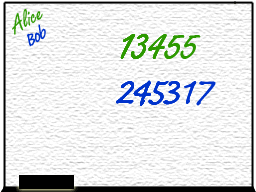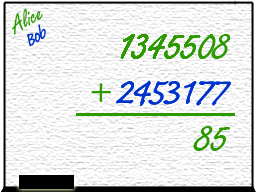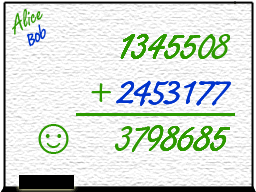
	1. If we're lucky, Bob might finish first and write his answer on the second line before Alice writes hers on the first line. Then Alice writes her number and sums it with Bob's and writes the correct answer. So far so good.
	2. But what if Alice was speedier than Bob? Then Alice writes her number first, and sums it with... nothing? Bob's number isn't there. For the sake of argument, suppose it was blank (in a computer that spot could contain random data). So Alice sums her number with nothing, returning a different, wrong number. Then Bob writes his number, but it has no influence on the output because it was not there in time. The output simply is wrong.
	3. We could have something in between happen. Since presumably Alice and Bob have equal ability to compute their numbers, this scenario is likely because they might not finish at exactly the same second. While Alice is halfway through writing her number, Bob begins writing his. Alice then can write the sum of what she sees of her number and his, but it's a race: she will begin writing the sum of the two numbers before Bob is finished writing his. Because the data she used was incomplete, yet again the output is wrong.

Now, if Alice and Bob are human beings, they would not be this literal. Alice, if she's polite, would wait for Bob if she was about to beat him to it. But the point is that, if these were processors A and B and the whiteboard is the shared memory, they would in fact be completely literal because they are just machines following instructions.

Then imagine if there were more than two numbers computed by as many others in the room. Alice and Bob and Charlie and Dave and Edna and Fred and George and so on would each have a number to write for Alice to sum together. It would be chaos. The output, even if the given problem was the same, would be different every time! If this were a computer, formerly the model of determinism and predictability, the machine would become completely unpredictable. We cannot even depend on a programming error to give the same wrong answer every time. If insanity is defined as expecting different results by doing the same thing, then we must be insane to program a machine that behaves this way.

In another example, to perform a Pascal's Triangle calculation with multiprocessing threads, a similar problem can occur in a simplistic shared memory solution. Extending the single-processor example, each processor reads overwrites an element of the array, one at a time, with the sum of the original and its neighboring element. The problem is that original values in memory might get overwritten by another processor, resulting in a wrong answer. (Using a old duplicate copy of the problem space would double the memory requirements, which is not always possible.) Without properly organizing the data and communication by partitioning the array and creating guard cells, using a threads approach can give wrong answers and be confusing.

In the addition example, the right thing to do is to explicitly manifest the dependency of Alice's final answer on Bob's completion of the second number. There are (at least) two different ways to go about that. Creators of typical shared memory implementations recognize that such machines are inherently nondeterminsitic, so their solution is to have the software programmer apply mechanisms to prune away this nondeterminism. Specifically, the shared memory with threads approach would it would use either a locking mechanism or a semaphore mechanism. Locking means that a processor would specify that second line as locked, preventing Alice from computing the sum until Bob unlocks it. Similarly, a semaphore means that Bob raises a flag to indicate to Alice to stop until Bob lowers the flag. Either way, if Bob doesn't lock the second line of the sum or raise the semaphore in time, then Alice will output a wrong answer again because it isn't there in time or is incomplete.

The above scenario, where Alice, Bob, Charlie, etc., are racing to write their numbers before Alice sums them is appropriately called a "race condition". This is a common problem when writing shared memory code. In principle it can be solved with any of these methods, but the additional issue with shared memory is that, when this condition occurs unforseen, the output is random and not repeatable, so diagnosing a problem when the symptom is never the same twice is very frustrating. There could even be extenuating circumstances that causes the right answer to appear on one system, but random answers to appear on another, further frustrating the writer. Such shared memory issues are very difficult to isolate and solve.

Why was Shared Memory Invented?

Why indeed? The reason is that, to the inexperienced, adding a processor to a single-processor computer seems like a simple solution to getting more computing power. Hook up the second processor to the same memory bus, and the job is done, right? As we can see by the above discussion, this becomes a difficult problem for the software writer. But shared memory is a problem for the hardware designer too. 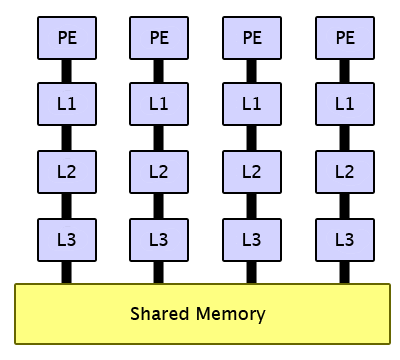Modern processors have level 1, level 2, and level 3 (or more) memory caches (some of which are connected) containing copies of pieces of main memory. This fact exacerbated the problem of maintaining the illusion of a single, unified, homogeneous shared memory accessible by all processors. A processor might, in cache, have a piece of data that no longer exists in main memory because it was just overwritten by another processor. So the hardware must be enhanced to maintain what's called "cache coherency". This problem, while arguably managable for two or four processors, rapidly grows for eight or more. Hardware becomes more complex and correspondingly expensive with the shared memory paradigm.

Distribute the Memory and Pass the Messages

The distributed memory with message passing approach is for Alice to wait for a phone call from Bob before attempting the sum. In fact, extending this analogy for message passing, Bob is in an entirely different room with his own whiteboard; when he's ready, he makes the call, and Alice, not Bob, writes the second line of the sum, so she knows his answer is ready, and she will produce the right output every time with complete determinism. If Charlie or Dave or Edna try to call, they'll be on call waiting until Alice has written Bob's answer, and she can take each of the other calls in order. Again, the interdependency in this problem is clear and explicit, and no one touches Alice's whiteboard but Alice.

As a practical matter, when a shared memory programmer wants to achieve the highest levels of performance and reliability, what do they do? They partition the memory and follow strict rules precisely when and where processors can share data. That's essentially the distributed memory with message passing model. Rather than emulate distributed memory with shared memory, perhaps it's simpler to just start assuming the distributed memory paradigm in the first place.

What also works is a hybrid approach. Small multiprocessing machines (usually SMP) of two, or perhaps four, processors each can be combined in a network suitable for distributed memory message passing. This solution takes advantage of multiprocessing within a box between just a few processors, but uses message passing to share data between boxes. In a sense, the multiprocessing approach becomes an orthogonal axis of parallelization from the distributed-memory message-passing approach: messages are passed at the highest level of partitioning, but multiple processors work within each node's partition. It works because the multiprocessing count is not too high so the advantages of quickly sharing memory can be used, yet message passing is applied to manage a large number of procesors. Likewise the hardware expense is low because each node has only a few processors. Software utilizing this approach is implemented in the Power Fractal application, which adds yet a third axis of parallelization with vector instructions.

It's Happened Before ...

The Great Schism of Parallel Computing in the 1990's centered around this debate between shared and distributed memory. Proponents of shared memory would argue that writing code for such systems was easier than using distributed memory with message passing. While for special examples the code would appear easier, but what these proponents do not seem to acknowledge is that most of the interesting problems have inherent dependency that cannot be eliminated. The above examples introduce fundamental issues that occur when applying the shared memory paradigm to such problems.

Silicon Graphics, Inc., (SGI) became the primary corporate advocate of the shared memory approach. While other companies like Intel, Cray, IBM, and Fujitsu abandoned shared memory in favor of distributed memory, SGI, at their peak, built impressive boxes with 256 processors all sharing memory at great expense. SGI developed technologies that we know today as OpenMP and, because their approach worked well for graphics because such applications are usually easy to parallelize, OpenGL. But, when asked to build 1024 processor systems, even SGI would have to build 4 nodes of 256 processors each connected via a network. Software and hardware layers would recreate the illusion of a shared memory system, but its speed would at best be limited by the network, just like for message passing. While today distributed memory systems operate with several thousand processors, SGI itself encountered a practical limit to the pure shared memory approach it advocated. So by the 21st century, what was SGI's fate? SGI was unable to produce technology sufficiently more powerful and more economic than its competitors in the HPC arena. Likewise, the corporate fortunes of SGI faired poorly, with stock prices under 50 cents per share after 2001, sinking below NYSE minimums. In 2006, SGI filed for Chapter 11 bankruptcy and major layoffs, leaving its stock worthless. Only in October does the company find new life after a complete financial overhaul.

In the meantime, clusters and supercomputers, well-represented at major supercomputing centers around the world, adopted the MPI standard on distributed memory hardware. Today, distributed memory MPI is the de facto standard at the San Diego Supercomputing Center, National Center for Supercomputing Applications, National Energy Research Scientific Computing Center, Lawrence Livermore National Laboratory and many more. Consider the annual reports of any of these organizations where they hilight the accomplishments they peform with their hardware. Today it goes without saying that these applications use the MPI and distributed memory approach. Even SGI's current product list includes the distributed-memory message-passing hardware design and MPI support.

... and It Will Happen Again In 2004, the microprocessor manufacturers industry-wide encountered a wall in the form of heat issues preventing higher clock speeds, with Intel delaying, then cancelling a 4 GHz chip. In 2005, Apple surprised the world when it decided to switch from PowerPC to Intel because it saw a growth path in Intel processors that IBM chose not to pursue with PowerPC. In 2006, Intel introduced their Core Duo processor, a chip that, as far as a software writer is concerned, has two processors. In addition, they announced that a four core chip is forthcoming and rumor has it that both AMD and Intel are slating 8- and 16-core chips for 2007 and beyond. Intel CEO Paul Otellini even previewed an 80-core chip as a way of pointing to a multicore future.

Where is this future? Two insights come to mind. First, Intel is advocating threads. By implication, what Intel is advocating essentially the shared memory approach championed by SGI in the 1990's. "Those who do not listen to history are doomed to repeat it." Intel is following the path SGI has already tread, only this time, because of Intel's microprocessor dominance, the entire personal computer industry is following the path to doom blazed by SGI. And we already know where SGI's old path ended: technological and financial ruin. Does this make sense?

The End is Near

The second insight regards Moore's law. The reign of the single-processor personal computer is over. While Dr. Gordon Moore's original observation of doubling transistor count every 18 to 24 months is holding true, by 2006 the popularized misinterpretation of Moore's law regarding doubling performance per processor is not. Intel, as well as IBM, AMD, and others, could not produce faster processors because the chips ran too hot. The fact that Intel saw it necessary to produce a chip with two Cores (as far as a software programmer is concerned a Core is a processor) to increase total performance is very telling. Essentially, Intel ran out of ideas to improve performance per chip save one: the technology of "copy and paste".

With the prospect of systems with four, eight, or more processors in a machine, it is left to the software programmers to use these systems effectively. Although industry is trending towards shared memory with threads, that is a path the HPC industry has already shown to be a mistake. Instead, the reader can learn from scientists, particularly those scientists who successfully apply massively parallel computing to major scientific problems, that distributed memory with message passing is the most successful approach to solve real-world problems using parallel computing. The need for programming parallel computers has arrived at our desktops, and lessons learned from scientists who apply computing can show us how if heeded.

For Additional Reading

Other tutorials on this web site show examples of code following these lessons. Parallelization - a discussion about the issues encountered when parallelizing code Parallel Zoology - compare and contrast parallel computing types: distributed, grid, and cluster computing and more Parallel Knock - an exhibition of basic message-passing in a parallel code Parallel Adder - an introduction to transforming a single-processor code with independent work into a parallel code Parallel Pascal's Triangle - an introduction to parallelizing single-processor code requiring local communication

Parallel Circle Pi - an introduction to load-balancing independent work in a parallel code Parallel Life - an introduction to parallelizing single-processor code running two-dimensional work requiring bidirectional local communication Visualizing Message Passing - a demonstration of message-passing visualization and what it can teach about a running parallel code You're welcome to read more about parallel computing via the Tutorials page.

A number of other references also make for interesting reading:

• The Problem with Threads - An excellent article by Edward A. Lee of UC Berkeley published in IEEE Computer describing in mathematical detail why programming threads on shared memory systems is a failed approach. He draws from real-world experience and warns readers to abandon threads entirely.

• In Search of Clusters by Gregory F. Pfister - This book is an excellent reference detailing all the different types of parallel computing and clusters. It describes difficulties and advantages of such systems from the perspective of hardware, software, and more. Particularly relevant is Chapter 9, sections 9.3 through 9.5, where Pfister describes solving a LaPlace equation beginning with a single processor, then shared memory, then message passing. Beginning with section 9.4.3 "Consistency and Chaos", he describes in detail multiple non-trivial strategies to wrestle the shared-memory approach to achieve simultaneously parallel speed up and the same answer twice in a row.

• "Chip wars go to the Core", published as "Cache, Cores, Clock Speed" on October 2, 2006 - InfoWorld's Tom Yager considers the consequences of moving to multiple cores, both by AMD and Intel. An insightful read, it questions today's industry trend. "AMD and Intel both face bus bottlenecks, and that's the bane of multicores."

• Chip Makers Turn to Multicore Processors - Published in the May 2005 issue of IEEE Computer, this article describes why the chip industry faced little choice but to go multicore to satisfy the original Moore's law.

• Multicore Eroding Moore's Law - The MacResearch site featured an op/ed article Multicore Eroding Moore's Law in 2007 questioning the industry's party line and highlighting the what multicore means for the computer industry as a whole. "The reign of the single-processor computer is over."

• Computing in a Parallel Universe - Brian Hayes' American Scientst Nov/Dec 2007 article gives an approachable discussion of the history of the computer chip industry and why the technology has scaled so well until now. It also cites Lee's article when describing the insanity of multithreading. Hayes writes: "As early as the 1960s, ... it was already widely believed that some form of 'massive parallelism' was the way of the future." "But if massive parallelism is really the way of the future, it can't remain behind the curtain forever. Everyone who writes software will have to confront the challenge of creating programs that run correctly and efficiently on multicore systems."

• Intel, Microsoft to back multicore research -
  • "Microsoft Chief Research and Strategy Officer Craig Mundie told CNET in May 2008 that the shift of the PC from a single processor to one with many processing engines is "probably the single most disruptive thing that we will have done in the last 20 or 30 years." "
  • "More cores can also add up to better performance, but to fully utilize multiple brains, software needs to be rewritten in ways that allow tasks to be split up and handled in parallel, a significant technical hurdle. "The software has to also start following Moore's Law," Intel fellow Shekhar Borkar said."

• Intel Nehalem Applying QuickPath Technology

  - In the Nehalem generation of Intel processors released in 2008: "Each processor has its own dedicated memory that it accesses directly... In cases where a processor needs to access the dedicated memory of another processor, it can do so through a high-speed Intel QuickPath Interconnect that links all the processors." - Intel white paper on Nehalem This solution is topologically equivalent to the distributed-memory architecture of MPI, which Intel diagrams for just two processors. While one might say "great minds think alike", here it is because they converge on a greater truth.

• Multicore is Bad News for Supercomputers - The November 2008 issue of IEEE Spectrum states: "With no other way to improve the performance of processors further, chip makers have staked their future on putting more and more processor cores on the same chip... The results are distressing. Because of limited memory bandwidth and memory-management schemes that are poorly suited to supercomputers, the performance of these machines would level off or even decline with more cores."

• Spending Moore's Dividend - James Larus of Microsoft Research writes in the May 2009 issue of Communications of the ACM:
  • "Multicore computers shift the burden of software performance from chip designers and processor architects to software developers."
  • "The era of steady growth of single-processor performance is over..."
  • "Applications that stop scaling with Moore's Law, either because they lack sufficient parallelism or because their developers no longer rewrite them, will be evolutionary dead ends."

• A View of the Parallel Computing Landscape - Authors from the Berkeley Parallel Computing Laboratory point out in the October 2009 issue of Communications of the ACM:
  • "The 2005 prediction was that clock rates should have exceeded 10GHz in 2008, topping 15 GHz in 2010." See Figure 1.
  • "After crashing into the power wall, architects were forced to find a new paradigm to sustain ever-increasing performance. The industry decided the only viable option was to replace the single power-inefficient processor with many... Hence, the leap to multicore is not based on a breakthrough in programming or architecture and is actually a retreat from the more difficult task of building power-efficient, high-clock-rate, single-core chips."
  • "Automatic parallelism doesn't work."
  • a quote from computing pioneer John Hennessy, President of Stanford University: "I would be panicked if I were in industry."
  • "Given the importance..., pessimism is not a sufficient excuse to sit on the sidelines. The sin is not lack of success but lack of effort."

• The Economist Babbage Podcast - May 18, 2011 - The Economist magazine's Babbage weekly podcast about science and technology discusses Gorden Moore's Law in light of the latest advances in three-dimensional chip construction. While they observe that this is the latest in a series of techniques chip makers use to maintain Moore's original observation about transistor densities, that leads them straight to the consequences for software. Some quotes:
  • "The problem there is that actually pushes the need for continual progress onto the software industry."
  • "What used to be quite an obscure programming problem for supercomputers and academics, which is 'how to you reliably and efficiently take advantage of massively parallel computers', is starting to become a real problem on the desktop."
  • "If software doesn't take advantage of these cores, the Intel can go on pushing out chips that have more and more processing cores inside them but the software won't be getting any faster, and we'll have this growing gap between what my computer is theoretically capable of and what it actually does."

  These words are spoken beautifully and succinctly in this excerpt.

• The Economist Parallel Bars article in their Technology Quarterly - June 4, 2011 - The Economist magazine's Technology Quarterly for June 2011 continues with even greater detail in their article "Parallel Bars". Some quotes:
  • "Making software run faster in the future will mean using parallel-programming techniques."
  • "What was once an obscure academic problem - finding ways to make it easy to write software that can take full advantage of the power of parallel processing - is rapidly becoming a problem for the whole industry. Unless it is solved, notes David Smith of Gartner, a market-research firm, there will be a growing divide between computers' theoretical and actual performance."
  • "Parallel-programming languages in particular tend to languish in academic obscurity. There are dozens of them - by one count, more than a hundred. None is popular." and yet "The DARPA challenge included the development of new parallel languages ..."
  • "... there has been so little progress in parallel programming, even though multicore chips have been widespread for five years."

Back to Top